| Sitemap Wissensch.+Technik Astronomie+Raumfahrt Wasser Medizin Blogs HTML-Tutorial Politik+Gesellschaft Wirtschaft+Ökonomie Harz+Oberharz Skandinavien Humor+Satire Sonstiges Downloads |
Grimm, H.:
pH-Wert in Wasser und wäßrigen Lösungen (Säuren, Basen, Salze, Salzgemische): ph-Berechnung und Ermittlung des pH mit dem Hägg-Diagrammhttp://www.wissenschaft-technik-ethik.de/wasser_ph.shtmlzuletzt aktualisiert am 02.03.2022 |
|
Inhaltsverzeichnis
Sonstige Verweise:
Definition und Berechnung des pH-Wertes Der pH-Wert ist der negative dekadische Logarithmus der Wasserstoffionenkonzentration c_H(+), gemessen in mol/L: pH = -(Log10(c_H(+)/(mol/L))) ....... (Gl.1) Eine Berechnung des pH für Wasser und wäßrige Lösungen von Elektrolyten (=Stoffe, die im Wasser z.T. in Ionen zerfallen = dissoziieren) ist über die dabei maßgeblichen chemischen Gleichgewichte möglich, wenn die Gleichgewichtskonstanten für die betreffenden Elektrolyte ("Dissoziationskonstanten") bekannt sind (z.B. aus Tabellen). Diese Konstanten sind sowohl stoff- alsauch temperaturabhängig. Die im Folgenden genannten Zahlenwerte gelten deshalb stets für einen bestimmten Stoff und eine bestimmte Temperatur (in der Regel 25°C). Für andere Temperaturen s. Tabellen im Anhang. Wer mit dem Rechnen mit Logarithmen nicht vertraut ist, sollte sich zunächst auf diesem Gebiet "schlau machen", da ohne diese Grundfertigkeit die im Folgenden aufgeführten Berechnungen nicht nachvollziehbar sind. Über die Maßeinheit mol kann sich der Leser unter http://www.wissenschaft-technik-ethik.de/wasser_loesung.shtml oder in der einschlägigen Fachliteratur informieren. 1. pH von reinem Wasser Das einfachste und grundlegendste Gleichgewicht im Wasser ist dessen eigener Zerfall in Ionen ("Eigendissoziation"): H2O <--> H(+) + OH(-) Zwischen H2O, H(+) und OH(-) stellt sich stets augenblicklich ein Gleichgewicht ein, und zwar in der Weise, dass das Produkt aus den Konzentrationen c_H(+) und c_OH(-) von H(+) bzw. OH(-) stets konstant ist: c_H(+) * c_OH(-) = const. Die betreffende Konstante wird als Gleichgewichtskonstante für die Eigendissoziation des Wassers bezeichnet, und üblicherweise mit dem Symbol KW versehen: c_H(+) * c_OH(-) = KW ....... (Gl.2) Der Wert für KW ist temperaturabhängig, und beträgt bei 25°C ziemlich genau 1*10^-14 mol^2/L^2. Eine Tabelle mit KW-Werten bei unterschiedlichen Temperaturen ist im Anhang wiedergegeben. Analog zu H(+)-Konzentration und pH-Wert wird auch der KW-Wert häufig als sein negativer dekadischer Logarithmus, bezeichnet als pKW-Wert, angewendet. In vollkommen reinem Wasser können H(+)- und OH(-)-Ionen ausschließlich durch die Eigendissoziation entstehen, folglich müssen die Konzentrationen beider Ionenarten gleich sein: c_H(+) = c_OH(-) Mit (Gl.2) folgt: KW = c_H(+)^2 = c_OH(-)^2 = 10^-14 mol^2/L^2 Daraus kann, unter Berücksichtigung von (Gl.1) der pH-Wert für reines Wasser berechnet werden: c_H(+) = KW^(1/2) = 10^-7 mol/L pH = -(Log10(10^-7)) = -(-7) = 7 Analog zum pH-Wert gibt es auch den pOH- und den pKW-Wert, die in Wasser und wäßrigen Lösungen mit dem pH-Wert in folgender Beziehung stehen: pH + pOH = pKW = 14 2. pH von wäßrigen Lösungen von Nichtelektrolyten Stoffe, die in wäßriger Lösung praktisch nicht in Ionen dissoziieren (Nichtelektrolyten) und auch keine Ionen an sich binden oder Ähnliches, beeinflussen den pH-Wert in der Regel nicht. Dies gilt etwa für Zucker oder Alkohol. Falls ein Nichtelektrolyt jedoch Verunreinigungen enthält, die beim Lösen in Wasser in Ionen zerfallen, können diese ionischen Verunreinigungen den pH-Wert beeinflussen. 3. pH von wäßrigen Lösungen von Elektrolyten 3.1 Allgemeines Wenn ein Elektrolyt in Wasser gelöst wird, zerfällt er mehr oder weniger stark in Ionen. So lange diese Ionen weder mit den vorhandenen H(+)- noch mit den OH(-)-Ionen reagieren und es sich bei ihnen nicht selbst um H(+) oder OH(-) handelt, beeinflussen auch gelöste Elektrolyte den pH-Wert nicht. 3.2 Säuren und Basen Säuren (können H(+) abspalten) und Basen oder "Laugen" (können OH(-) abspalten) beeinflussen den pH direkt. Salzsäure z.B. zerfällt in Wasser: HCl <--> H(+) + Cl(-) Das erhöht natürlich die H(+)-Konzentration und verringert damit den pH-Wert. Die erhöhte H(+)-Konzentration führt dazu, dass ein Teil der aus dem Selbstzerfall des Wassers vorhandenen OH(-)-Ionen wieder mit H(+) zu Wasser (zurück)reagiert und sich dadurch die OH(-)-Konzentration verringert, bis die Gleichgewichtsbedingung für die Wasserdissoziation (Gl.2) wieder erfüllt ist. Ein Rechenbeispiel: Die HCl-Konzentration sei 10^-3 mol/L (Das sind bei HCl knapp 37 mg/l, also nicht gerade viel). HCl als eine der stärksten Säuren zerfällt praktisch vollständig in seine Ionen, so dass folglich etwa 10^-3 mol/L H(+) freigesetzt werden. Die zusätzlich wegen der Eigendissoziation des Wassers vorhandenen H(+) fallen demgegenüber mengenmäßig nicht ins Gewicht und können deshalb hier vernachlässigt werden, was die folgenden Berechnungsschritte vereinfacht. Mit (Gl.2) folgt: c_OH(-) * 10^-3 mol/L = 10^-14 mol^2/L^2 c_OH(-) = 10^-11 mol/L pH = 3 pOH = 11 Noch ein Beispiel: Welchen pH hat eine 0,2%ige (also schon ziemlich verdünnte) Salzsäure? Wir setzen für die Dichte ungefähr 1 kg/L an, und erhalten so eine HCl-Konzentration von ca. 2 g/L. Wegen des Molgewichts der HCl von 36,5 g/mol ist ihre molare Konzentration c_HCl = 2 g/L / 36,5 g/mol = 0,055 mol/L = 5,5 * 10^-2 mol/L. Da nahezu die gesamte HCl dissoziiert, und demnach pro 1 HCl nahezu 1 H(+) abgespalten wird, ist die H(+)-Konzentration näherungsweise ebenso groß wie die HCl-Konzentration: c_H(+) = 5,5 * 10^-2 mol/L und damit ist der pH: pH = -(Log10(5,5 * 10^-2)) = 1,26 Im Prinzip genauso verhält es sich mit Lösungen einer "starken" Base, also einer Base, die praktisch vollständig in ihre Ionen zerfällt, z.B. Natriumhydroxid (NaOH): NaOH <--> Na(+) + OH(-) Bei einer Konzentration von 10^-3 mol/L NaOH entstehen nahezu 10^-3 mol/L OH(-)-Ionen. pOH = 3 Und, da immer pH + pOH = ca. 14: pH = 11 Bei sog. "schwachen" Säuren und Basen sind die Verhältnisse nicht so einfach. Bei ihnen hängt es von den äußeren Umständen (aktueller pH, Temperatur, Konzentration) ab, wie groß der Anteil ihrer H(+)-Ionen ist, den sie in Lösung abgeben. Um das Ganze rechnerisch in den Griff zu bekommen, muss man ihre Gleichgewichtskonstanten ("Säurekonstanten", "Säuredissoziationskonstanten") kennen. Es gibt sogenannte "einbasige" Säuren, die nur ein H(+)_ion abspalten können, und "mehrbasige" Säuren, die 2, 3 oder mehr H(+)-Ionen abspalten können. Beispiele für einbasige Säuren (im Folgenden allgemein als HX bezeichnet) sind: HCl (Salzsäure) HCH3COO (Essigsäure) HNO3 (Salpetersäure) H(OOC-H) (Ameisensäure) HCN (Cyanwasserstoffsäure, "Blausäure") Beispiele für zweibasige Säuren (im Folgenden allgemein als H2Y bezeichnet): H2SO4 (Schwefelsäure) H2SO3 (Schweflige Säure) H2CO3 (Kohlensäure) H2(OOC)2 (Oxalsäure) H2S (Schwefelwasserstoff) Beispiele für dreibasige Säuren (im Folgenden allgemein als H3Z bezeichnet): H3PO4 (Phosphorsäure) H3BO3 (Borsäure) H3(C6H5O7) (Citronensäure) Auch unter den Basen gibt es ein- und mehrwertige Vertreter: NaOH (Natronlauge, einwertig) KOH (Kalilauge, einwertig) NH4OH (Ammoniumhydroxid, einwertig) Ca(OH)2 (Calciumhydroxid, "gelöschter Kalk", zweiwertig) Fe(OH)3 (Eisen(III)hydroxid, dreiwertig) Während einbasige Säuren lediglich in H(+) und X(-) dissoziieren können, dissoziieren mehrbasige Säuren in mehreren Schritten: H2Y <--> H(+) + HY(-) HY(-) <--> H(+) + Y(2-) und H3Z <--> H(+) + H2Z(-) H2Z(-) <--> H(+) + HZ(2-) HZ(2-) <--> H(+) + Z(3-) Dabei bildet sich, je nach dem sich einstellenden pH-Wert, ein Gleichgewicht zwischen den Konzentrationen der unterschiedlich "deprotonierten" Säurereste (z.B. H3Z, H2Z(-), HZ(2-) und Z(3-)) aus. Um das Gesamtgleichgewicht ermitteln zu können, werden zunächst die Gleichgewichtsverhältnisse für die einzelnen Dissoziationsstufen betrachtet. Für eine einbasige Säure HX gibt es nur eine Dissoziationsstufe, und das Gleichgewicht stellt sich gemäß folgender Gleichung ein: c_H(+) * c_X(-) / c_HX = KS1 ....... (Gl.3) mit c_H(+), c_X(-): Konzentrationen von H(+) und X(-) in mol/L c_HX: Konzentration des nicht dissoziierten Säureanteils KS1: Säuredissoziationskonstante für die 1. Dissoziationsstufe (Da es für einbasige Säuren nur eine einzige Dissoziationsstufe, und folglich nur eine einzige Dissoziationskonstante gibt, wird KS1 in diesem Fall häufig einfach als KS bezeichnet.) Bei der Dissoziation mehrbasiger Säuren stellen sich die folgenden Einzelgleichgewichte ein: c_H(+) * c_HY(-) / c_H2Y = KS1 ....... (Gl.4) c_H(+) * c_Y(2-) / c_HY(-) = KS2 ....... (Gl.5) bzw. c_H(+) * c_H2Z(-) / c_H3Z = KS1 ....... (Gl.6) c_H(+) * c_HZ(2-) / c_H2Z(-) = KS2 ....... (Gl.7) c_H(+) * c_Z(3-) / c_HZ(2-) = KS3 ....... (Gl.8) Im Gegensatz zu c_HX, c_H2Y und c_H3Z die für den nicht dissoziierten Anteil der Säure stehen, bedeuten c_X, c_Y und c_Z im Folgenden die Gesamtkonzentration des betreffenden Säurerests in allen jeweils möglichen Protonierungsgraden: c_X = c_HX + c_X(-) ....... (Gl.9) c_Y = c_H2Y + c_HY(-) + c_Y(2-) ....... (Gl.10) c_Z = c_H3Z + c_H2Z(-) + c_HZ(2-) + c_Z(3-) ....... (Gl.11) Soweit lediglich die betreffende Säure oder eines ihrer Salze gelöst wurde, und somit die einzige Quelle für die betreffenden unterschiedlich protonierten Säurereste ist, entspricht c_X, c_Y bzw. c_Z der Stoffmenge der Säure bzw. des Salzes in mol, die bzw. das in Wasser zu 1 L Lösung gelöst wurde. Analog zur Dissoziation von Säuren in H(+) und Säurerest dissoziieren Basen in Basenrest und OH(-). Es gelten analoge Gleichgewichtsbedingungen. Die Gleichgewichtskonstanten für den Basenzerfall werden als KB1, KB2 usw. bezeichnet. Für eine gemeinsame Gleichgewichtsbetrachtung von gemeinsam gelöster Säure und Base müssen die KB-Werte in KS-Werte umgerechnet werden oder umgekehrt. Es gilt für eine bestimmte Substanz Sz (Säure oder Base) in der n-ten Dissoziationsstufe: KSn(Sz) * KBn(Sz) = KW = 10^-14 mol^2/L^2 .. (Gl.12) 3.3 Hägg-Diagramm Aus den Gleichgewichtsbedingungen (Gl.3) bis (Gl.8) und den Säurerestbilanzen (Gl.9) bis (Gl.11) lassen sich Gleichungen ableiten, mit deren Hilfe sich die Konzentrationen der unterschiedlich protonierten Säurereste bei gegebenem c_X bzw. c_Y bzw. c_Z für jede H(+)-Konzentration berechnen lassen (Ableitung s. Anhang). Trägt man die errechneten Konzentrationen der unterschiedlich protonierten Säurereste in logarithmischem Maßstab über dem pH-Wert auf, erhält man ein sogenanntes "Hägg-Diagramm". In nicht zu komplizierten Fällen kann unter Berücksichtigung logischer Zusammenhänge zwischen den Konzentrationen der H(+)-Ionen und der unterschiedlich protonierten Säurereste der pH-Wert auf relativ einfache Weise ermittelt werden. Dabei besteht ein großer Vorteil dieser Methode darin, dass sich ein Hägg-Diagramm, wenn man das Prinzip begriffen hat, notfalls auch ohne Computer oder langwierige Berechnungen mit einiger Genauigkeit rasch auf einem Blatt Millimeterpapier von Hand erzeugen lässt. Im Folgenden soll der Umgang mit dem Hägg-Diagramm anhand ausgewählter Beispiele Schritt für Schritt erläutert werden. Das Prinzip, nach dem ein Hägg-Diagramm notfalls von Hand konstruiert werden kann, sollte bei Betrachtung der Beispiele leicht zu erkennen sein. 3.3.1 Reines Wasser Der einfachste Fall ist reines Wasser. Wegen der Definition des pH-Wertes und seines Zusammenhangs mit dem pOH-Wert ergeben sich für c_H(+) und c_OH(-) stets die in Bild 1 gezeigten Verläufe, auch dann, wenn das Wasser gelöste Substanzen und Ionen enthält: 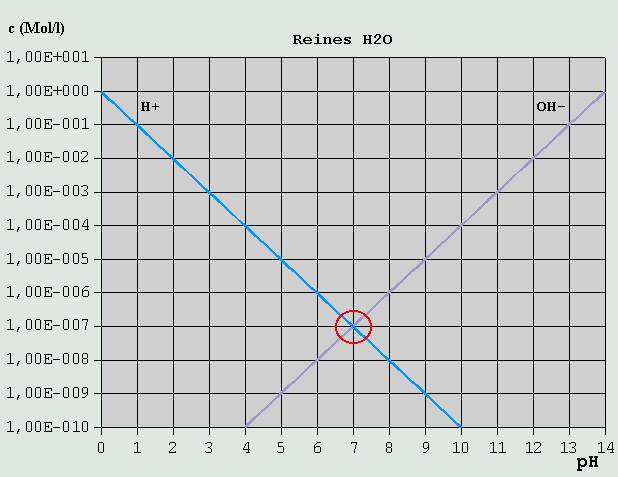 Bild 1: Hägg-Diagramm für reines Wasser Um aus Bild 1 den pH für reines Wasser zu ermitteln, muss lediglich eine Mengenbilanz der vorhandenen gelösten Ionen aufgestellt werden. In diesem Fall sind dies lediglich H(+) und OH(-), deren Konzentrationen in reinem Wasser logischerweise praktisch gleich sind (2. Eigendissoziationsstufe: OH(-) <--> H(+) + O(2-) kann vernachlässigt werden). Dies ist offensichtlich am Schnittpunkt der beiden Konzentrationsverläufe der Fall, der bei pH = 7,0 liegt. 3.3.2 Starke Säuren Als nächsten einfachen Fall betrachten wir eine 0,1-molare HCl-Lösung. Wegen des exorbitant hohen KS der HCl ist die Konzentration nichtdissoziierter HCl auch bei niedrigen pH-Werten äußerst gering. 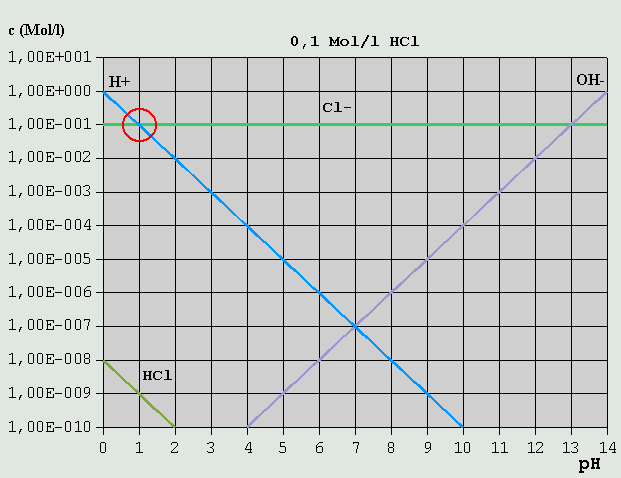 Bild 2: Hägg-Diagramm für eine 0,1M-HCl-Lösung Da H(+) hier sowohl durch die Eigendissoziation des Wassers in H(+) + OH(-), alsauch durch die Dissoziation der HCl in H(+) + Cl(-) entsteht, lautet hier die Bilanzgleichung: c_H(+) = c_OH(-) + c_Cl(-) Wie man leicht sieht, ist diese Bedingung nur in einem Punkt erfüllt (auch hier wieder rot eingekreist), der bei pH = 1,0 liegt. c_OH(-) ist hier so verschwindend gering, dass es vollkommen vernachlässigt werden kann. 3.3.3 Starke Basen Ähnlich verhält es sich mit einer 0,1M-NaOH-Lösung. 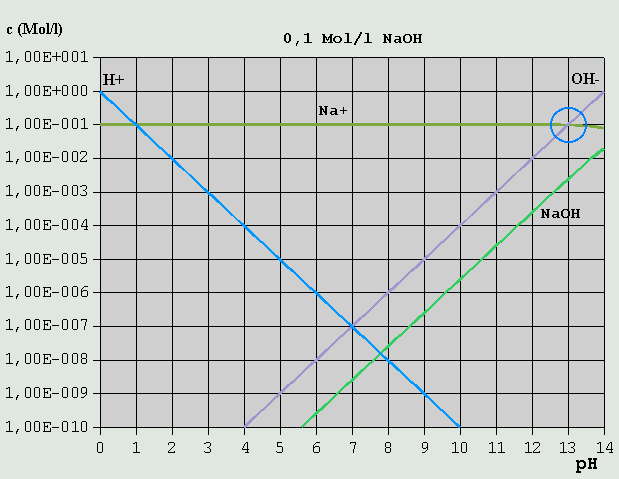 Bild 3: Hägg-Diagramm für eine 0,1M-NaOH-Lösung Aus der Bilanzgleichung c_OH(-) = c_H(+) + c_Na(+) ergibt sich der passende pH bei pH = ca. 13,0 (blauer Kreis). c_H(+) kann in diesem Fall vernachlässigt werden (nur ca. 10^-13 Mol/l). 3.3.4 Salze starker Säuren mit starken Basen Ein Salz einer starken Säure und einer starken Base ist z.B. Kochsalz (NaCl, aus HCl und NaOH durch Neutralisation gebildet). 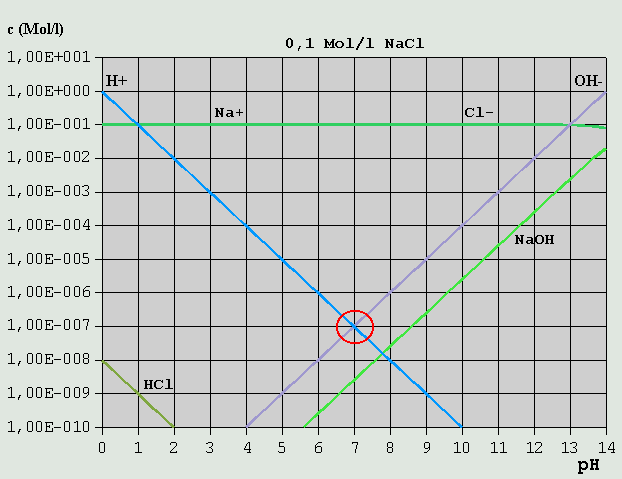 Bild 4: Hägg-Diagramm für eine 0,1M-NaCl-Lösung Die erforderliche Bilanzgleichung ergibt sich aus der Überlegung, dass einerseits Cl(-) mit H(+) zu (wenig) HCl, und Na(+) mit OH(-) zu (wenig) NaOH reagiert: c_H(+) + c_HCl = c_OH(-) + c_NaOH Die Konzentrationen von HCl und NaOH sind gegenüber denen von H(+) und OH(-) über den gesamten pH-Bereich vernachlässigbar gering. Daher gilt hier wieder, wie beim reinen Wasser: c_H(+) = c_OH(-) Der pH-Wert ist also 7,0. Salze aus starken Säuren und starken Basen beeinflussen normalerweise den pH-Wert praktisch nicht. 3.3.5 Schwache Säuren und ihre Salze mit starken Basen Die so genannten schwachen Säuren sollen anhand des Beispiels Essigsäure besprochen werden. Essigsäure zerfällt, im Prinzip wie Salzsäure, nach: HCH3COO <--> H(+) + CH3COO(-) 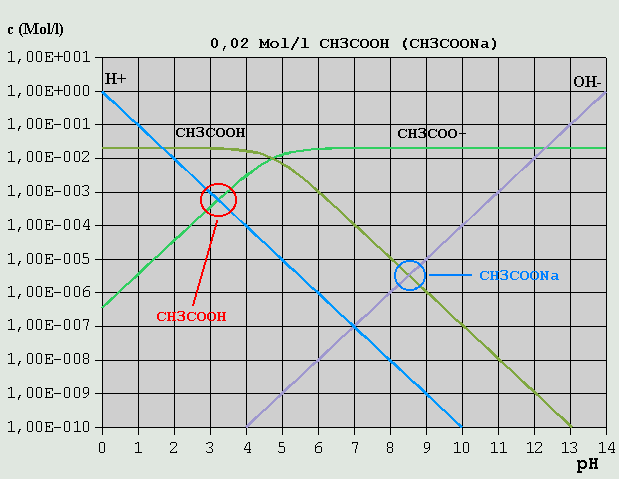 Bild 5: Hägg-Diagramm für eine 0,02M-HCH3COO-Lösung bzw. für eine 0,02M-NaCH3COO-Lösung Im Gegensatz zur Salzsäure erfolgt jedoch wegen des vergleichsweise hohen pKS-Wertes die Dissoziation erst ab entsprechend hohen pH-Werten in erheblichem Umfang. Analog zur Salzsäure lautet die Bilanzgleichung: c_H(+) = c_OH(-) + c_CH3COO(-) Wie im Diagramm leicht erkennbar ist, kann c_OH(-) vernachlässigt werden, so dass wegen c_H(+) = c_CH3COO(-) der pH-Wert am Schnittpunkt der betreffenden Konzentrationskurven zu etwa 3,2 abgelesen werden kann. Ein Salz der Essigsäure mit einer starken Base (im Beispiel: Natriumacetat = NaCH3COO) zerfällt in wäßriger Lösung in Na(+) und CH3COO(-). Analog zur NaCl-Lösung folgt die erforderliche Bilanzgleichung aus der Überlegung, dass einerseits CH3COO(-) z.T. mit H(+) zu HCH3COO, und Na(+) z.T. mit OH(-) zu NaOH reagiert: c_H(+) + c_HCH3COO = c_OH(-) + c_NaOH Dabei kann c_NaOH (hier nicht im Diagramm eingezeichnet, s. Diagramm NaCl) gegenüber c_OH(-), und c_H(+) gegenüber c_HCH3COO vernachlässigt werden: c_HCH3COO = c_OH(-) Am Schnittpunkt der betreffenden Konzentrationsverläufe kann der pH-Wert zu etwa 8,5 abgelesen werden. Erwähnt sei auch der Fall eines Gemisches aus gleichen Mengen gleich konzentrierter Essigsäure- und Natriumacetat-Lösung. Die Bilanzgleichung lautet: c_H(+) + c_HCH3COO = c_OH(-) + c_CH3COO(-) + c_NaOH Wie leicht zu erkennen ist, können gegenüber c_HCH3COO und c_CH3COO(-) alle anderen Ionensorten vernachlässigt werden, so dass der pH-Wert am Schnittpunkt der dazugehörigen Konzentrationsverläufe als ca. 4,7 bestimmt werden kann. Dies ist der pKS-Wert für Essigsäure. Zu beachten ist, dass bei entsprechend stark verdünnten Lösungen u.U. andere Konzentrationsverhältnisse vorherrschen, so dass weniger oder andere Konzentrationen vernachlässigt werden können. Um sich dies zu veranschaulichen, verschiebe man die Kurven von HCH3COO und CH3COO(-) im Geiste senkrecht nach unten, bis z.B. die c_H(+)- und die c_HCH3COO-Kurve sehr nahe beieinander oder aufeinander liegen.. 3.3.6 Schwache Basen und ihre Salze mit starken Säuren Analog zur schwachen Säure und ihrem Salz mit einer starken Base kann auch im umgekehrten Fall verfahren werden, nämlich bei einer schwachen Base und ihrem Salz mit einer starken Säure. Im folgenden Beispiel ist Ammoniak (NH3, bzw. NH4OH) die schwache Base und HCl die starke Säure: 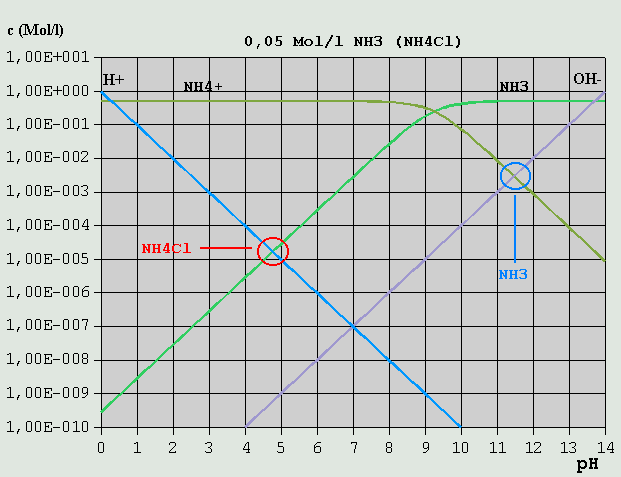 Bild 6: Hägg-Diagramm für eine 0,5M-NH3-Lösung bzw. für eine 0,5M-NH4Cl-Lösung Aus NH4OH <--> NH4(+) + OH(-) (*) folgt die Bilanzgleichung c_NH4(+) + c_H(+) = c_OH(-) c_H(+) kann im vorliegenden Fall vernachlässigt werden, so dass sich der pH am Schnittpunkt der Kurven für c_NH4(+) und c_OH(-) zu ca. 11,5 ablesen lässt. Für die NH4Cl-Lösung gilt NH4(+) <--> H(+) + NH3 c_H(+) = c_NH3 + c_OH(-) Im Beispiel ist c_OH(-) vernachlässigbar gegenüber c_NH3, und der pH ist beim Schnittpunkt der Kurven für c_H(+) und c_NH3 abzulesen, hier bei ca. 4,7. Wird eine 0,5M-NH3-Lösung mit HCl titriert, ändert sich dabei bis zum Erreichen des Äquivalenzpunktes der pH von 11,5 auf 4,7. Welchen Wert hat der pH, wenn gerade die Hälfte des NH3 bei der Titration umgesetzt ist? Dann ist c_NH3 = c_NH4(+) (c_H(+) und c_OH(-) vernachlässigt) und der pH liegt am Schnittpunkt der betr. Kurven bei ca. 9,3. (*) Anstelle von NH4OH kann ebensogut NH3 + H2O stehen. Für die pH-Ermittlung ist dies jedoch belanglos. 3.3.7 Mehrbasige Säuren Mehrbasige Säuren können mehr als 1 H(+) pro Molekül abspalten. Die Abspaltung geschieht (Beispiel Phosphorsäure) in entsprechend vielen Schritten: 1.) H3PO4 <--> H(+) + H2PO4(-) 2.) H2PO4(-) <--> H(+) + HPO4(2-) 3.) HPO4(2-) <--> H(+) + PO4(3-) Eine Lösung von Phosphorsäure oder von einem ihrer Salze enthält immer (in sehr unterschiedlicher Konzentration) alle möglichen Varianten (H3PO4, H2PO4(-), HPO4(2-) und PO4(3-)). Wie in (Gl.6) bis (Gl.8) dargelegt, gibt es bei der dreibasigen Phosphorsäure 3 unterschiedliche Dissoziationskonstanten und ihre p-Werte. Durch eine Berechnung der Konzentrationskurven erhält man das folgende Diagramm: 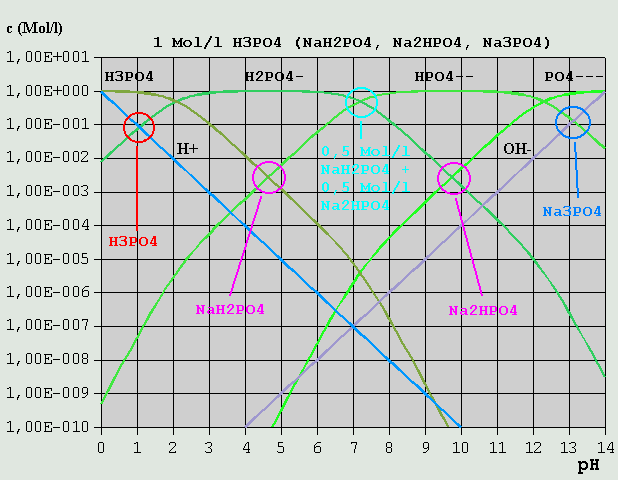 Bild 7: Hägg-Diagramm für Phosphorsäure und ihre Salze Um die Bilanzgleichung aufzustellen, verfährt man folgendermaßen: Die eingesetzte Variante kommt in der Bilanzgleichung nicht vor. Bei einer Lösung von NaH2PO4 ist dies z.B. das H2PO4(-). H(+) und alle vorkommenden Varianten mit höherem H-Gehalt (weniger dissoziiert) als die eingesetzte Ionenart kommen auf die linke Seite der Gleichung. OH(-) und die übrigen Varianten kommen auf die rechte Seite. Für NaH2PO4 ist die Bilanzgleichung demnach: c_H(+) + c_H3PO4 = c_OH(-) + c_HPO4(2-) + c_PO4(3-) (c_NaOH ist hierbei von vornherein vernachlässigt und nicht mit aufgeführt.) Im vorliegenden Hägg-Diagramm für eine 1M-Phosphorsäure- bzw. Phosphat-Lösung ist sofort ersichtlich, dass alle Konzentrationen außer c_H3PO4 und C_HPO4(2-) vernachlässigt werden können (H2PO4(-) kommt ja in der Bilanzgleichung nicht vor). Der pH liegt also am Schnittpunkt der betreffenden Kurven (pH = 4,6). Bei einer 0,005M-NaH2PO4-Lösung liegen die Verhältnisse etwas anders (s. Bild 8). c_H(+) kann nicht mehr vernachlässigt werden, und es gilt der Schnittpunkt der kurzen braunen Linie, die die Summe aus c_H(+) und c_H3PO4 repräsentiert, und der c_HPO4(2-)-Kurve. Die kurze braune Linie auf der rechten Seite repräsentiert die Summe aus c_OH(-) und c_PO4(3-). 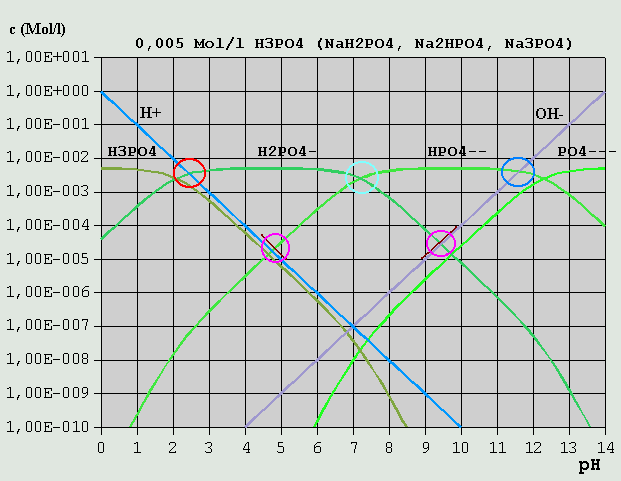 Bild 8: Hägg-Diagramm für Phosphorsäure und ihre Salze in stärker verdünnter Lösung Der Leser möge übungshalber selbst einmal die Bilanzgleichungen für Lösungen von H3PO4 Na2HPO4 Na3PO4 aufstellen (Lösungen siehe unten). Wegen der besonderen Bedeutung der Kohlensäure und ihrer Salze, der Carbonate, in der Natur und für die Lebensvorgänge, soll auf diese Stoffgruppe hier noch einmal gesondert eingegangen werden. In Wasser gelöstes CO2 reagiert in einer langsamen Reaktion (mehrere Sekunden) zu einem geringen Teil mit Wasser zu einer nicht sehr stabilen Säure, der Kohlensäure, die dann in 2 Stufen dissoziiert: CO2 + H2O <--> H2CO3 (Bildung der Kohlensäure) H2CO3 <--> H(+) + HCO3(-) HCO3(-) <--> H(+) + CO3(2-) (Es ist inzwischen gelungen, die Existenz von Kohlensäure in wäßriger Lösung auch mit Hilfe spektroskopischer Methoden nachzuweisen. Die bis Mitte Februar 2006 an dieser Stelle vertretene Auffassung, die Existenz von H2CO3 sei bisher nicht nachgewiesen, wird hiermit revidiert.) Die Salze der Kohlensäure, die Carbonate (z.B. Soda = Natriumcarbonat = Na2CO3 und Natron = Natriumhydrogencarbonat = NaHCO3), lassen sich leicht in reiner Form darstellen. Für die pH-Berechnung von CO2-Lösungen, bei denen in der Regel die Konzentration des gelösten CO2 bekannt ist, ist es am praktischsten, die Gleichgewichtskonstanten der H2CO3-Bildung und der H2CO3-Dissoziation zu einer einzigen Gleichgewichtskonstante für CO2 zusammenzufassen, und somit die saure Reaktion von in Wasser gelöstem CO2 formal durch die Reaktionen CO2 + H2O <--> H(+) + HCO3(-) und CO2 + OH(-) <--> HCO3(-) ....... (Gl.13) zu beschreiben. Die u.a. pKS-Werte für CO2 sind solche zusammengefassten Gleichgewichtswerte. Bei (Gl.13) werden OH(-)-Ionen durch CO2 "weggefangen", so dass Wassermoleküle dissoziieren, um das H(+)-OH(-)-Gleichgewicht wieder herzustellen, wobei entsprechend viele H(+)-Ionen gebildet werden. Die Interpretation des Hägg-Diagramms für eine 0,05M-Lösung von CO2 oder eines seiner Salze sei dem Leser selbst überlassen. 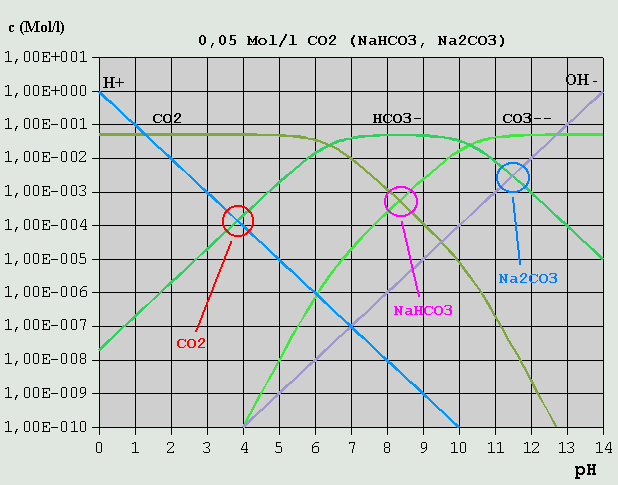 Bild 9: Hägg-Diagramm für CO2 und Carbonate 3.3.8 Mischungen verschiedener Salze einer Säure Im Hägg-Diagramm für eine 1M-Phosphorsäure/Phosphat-Lösung ist u.A. auch der pH einer Mischung aus je 0,5 Mol/l NaH2PO4 und Na2HPO4 eingezeichnet (s. Bild 7). Da diese Ionenarten alle übrigen in der Lösung in ihrer Konzentration weit übertreffen, bestimmen sie auch den pH-Wert, der sich somit am Schnittpunkt von c_H2PO4(-) und c_HPO4(2-) zu 7,2 ablesen lässt. Abschließend soll noch eine Lösung unterschiedlicher Konzentrationen zweier Salze betrachtet werden.  Bild 10: Hägg-Diagramm für ein Gemisch unterschiedlicher Konzentrationen von HCO3(-) und CO3(2-) Im Beispiel ist die CO3(2-)-Konzentration 4 mal so hoch wie die HCO3(-)-Konzentration. Da die übrigen beteiligten Ionenarten sämtlich vernachlässigt werden können, lautet die Bilanzgleichung einfach: 4 * c_HCO3(-) = ca. c_CO3(2-) Wegen des logarithmischen Maßstabs im Hägg-Diagramm wird ein Faktor (im Beispiel = 4) durch eine Strecke konstanter Länge repräsentiert (senkrechte rote Strecke auf der Grafik). Um diese Strecke muss folglich beim zu ermittelnden pH-Wert die c_CO3(2-)-Kurve über der c_HCO3(-)-Kurve liegen. Im Beispiel ergibt sich ein pH von 10,9. Anhang 1. KW- und pKW-Werte für Wasser in mol^2/L^2 pKW = -(Log10(KW/(mol^2/L^2))) Temp.(°C) KW pKW =================================== 0 1,14 * 10^-15 14,944 5 1,85 * 10^-15 14,734 10 2,92 * 10^-15 14,535 15 4,51 * 10^-15 14,346 20 6,81 * 10^-15 14,167 25 1,01 * 10^-14 13,997 30 1,47 * 10^-14 13,833 40 2,92 * 10^-14 13,535 50 5,47 * 10^-14 13,262 60 9,61 * 10^-14 13,017 2. Neg. dekad. Logarithmen von Dissoziationskonstanten wichtiger Säuren und Basen für wäßrige Lösungen (Auch bei Basen sind hier die Säurekonstanten angegeben, die aus den Basenkonstanten mit pKs = pKW - pKb errechnet werden können. Die z.T. etwas widersprüchlichen Angaben resultieren aus der Verwendung unterschiedlicher Quellen und zeigen, dass eine Angabe der Werte mit 2 Nachkommastellen eigentlich nicht gerechtfertigt ist.) Stoff pKS1 pKS2 pKS3 Temp. =============================================== HCl -7 25°C HBr -9 25°C HJ -9,5 25°C HCN 9,31 25°C HF 3,17 25°C HF 3,45 25°C HNO3 -1,3 30°C CO2 6,37 10,25 25°C H2S 7,04 11,96 18°C H2S 6,1 11,4 20°C H2SO3 1,81 6,91 18°C H2SO4 0(ca.) 1,9 20°C H3PO4 12,67 18°C H3PO4 2,13 7,21 20°C H3PO4 12,3 ? H3PO4 2,12 7,21 25°C NaOH 14,6(ca.) 25°C NH3 9,74 10°C NH3 9,40 20°C NH3 9,09 30°C NH3 8,81 40°C Ca(OH)2 11,6 12,6 25°C HCOOH 3,75 20°C HCH3COO 4,75 20°C Propans. 4,87 20°C Butans. 4,81 20°C Chloressigs. 2,85 25°C Dichloressigs. 1,48 25°C Trichloressigs. 0,70 25°C Jodessigs. 3,12 25°C Phenylessigs. 4,28 18°C Vinylessigs. 4,34 25°C Oxals. 1,23 4,19 25°C Malons. 2,82 5,70 20°C Bernsteins. 4,22 5,64 20°C Acryls. 4,25 25°C l-Aepfels. 3,41 4,86 20°C Ascorbins. 4,10 24°C Ascorbins. 11,79 16°C Benzoes. 4,19 25°C Harnsaeure 3,89 12°C Milchs. 3,08 100°C Terephthals. 3,51 25°C a-Weins. 2,98 4,34 25°C Meso-Weins. 3,22 4,82 25°C Zitronens. 3,14 4,77 6,39 20°C Phenol 9,89 20°C Methanol 17 18°C Glykol 14,2 19°C Glykol 14,2 25°C 3. Quellen: D'Ans-Lax, Taschenbuch für Chemiker und Physiker, Band 1, 3. Auflage, Springer Weast, Handbook of Chemistry and Physics, 64th Edition, CRC Press 4. Ableitung der Gleichungen zur Erstellung eines Hägg-Diagramms In diesem Abschnitt Verwendete Formelzeichen: X, Y, Z: Ein- bzw. zwei- bzw. dreibasiger Säurerest c_Kpn: Konzentration der Komponente Kpn KS1, KS2, KS3: Dissoziationskonstanten für 1. bzw. 2. bzw. 3. Dissoziationsstufe a) Einbasige Säuren HX <--> H(+) + X(-) KS1 = c_H(+) * c_X(-) / c_HX ....... (Gl.A1) Aus (Gl.A1) folgen 2 Gleichungen, die die Abhängigkeit der Konzentration eines protonierten Säurerests von der des jeweils anderen beschreibt: c_HX = c_X(-) * (c_H(+) / KS1) ....... (Gl.A2) c_X(-) = c_HX * (KS1 / c_H(+)) ....... (Gl.A3) In der Bilanzgleichung c_HX + c_X(-) = c_X ....... (Gl.A4) wird jeweils unter Berücksichtigung von (Gl.A2) bzw. (Gl.A3) eine der Konzentrationen durch den mathematischen Ausdruck für die andere ersetzt. In (Gl.A4) wird gemäß (Gl.A3) c_X(-) durch c_HX * KS1 / c_H(+) ersetzt: c_HX + c_HX * KS1 / c_H(+) = c_X Auflösen der Gleichung nach c_HX ergibt: c_HX * (1 + KS1 / c_H(+)) = c_X c_HX = c_X / (1 + KS1 / c_H(+)) Adäquat verfährt man mit (Gl.A4) und (Gl.A2) und erhält: c_X(-) = c_X / (c_H(+) / KS1 + 1) b) Zweibasige Säuren Bei zweibasigen Säuren gibt es 2 Gleichgewichtskonstanten: KS1 = c_H(+) * c_HY(-) / c_H2Y ....... (Gl.B1) KS2 = C_H(+) * c_Y(2-) / c_HY(-) ....... (Gl.B2) Die Multiplikation beider Gleichungen miteinander ergibt: KS1 * KS2 = c_H(+)^2 * c_Y(2-) / c_H2Y ....... (Gl.B3) Durch sinnvolle Kombinationen von jeweils 2 der (Gl.B1) bis (Gl.B3) erhält man 3 mal 2 Gleichungen, die die Abhängigkeit der Konzentration von jeweils einem protonierten Säurerest von einer der jeweils 2 anderen beschreibt: c_H2Y = c_HY(-) * c_H(+) / KS1 ....... (Gl.B4) c_H2Y = c_Y(2-) * c_H(+)^2 / (KS1 * KS2) ....... (Gl.B5) c_HY(-) = c_H2Y * KS1 / c_H(+) ....... (Gl.B6) c_HY(-) = c_Y(2-) * c_H(+) / KS2 ....... (Gl.B7) c_Y(2-) = c_HY(-) * KS2 / c_H(+) ....... (Gl.B8) c_Y(2-) = c_H2Y * KS1 * KS2 / c_H(+)^2 ....... (Gl.B9) In der Bilanzgleichung c_H2Y + c_HX(-) + c_Y(2-) = c_Y ....... (Gl.B10) werden nacheinander jeweils 2 der links vom Gleichheitszeichen stehenden Konzentrationen durch entsprechende Ausdrücke aus 2 der Gleichungen (Gl.B4) bis (Gl.B9) ersetzt, so dass 3 Gleichungen entstehen, die jeweils nur noch eine Konzentration eines protonierten Säurerests als Unbekannte enthält. Aus (Gl.B10) folgt z.B. durch Kombination mit (Gl.B6) und (Gl.B9): c_H2Y + c_H2Y * (KS1 / c_H(+)) + c_H2Y * (KS1 * KS2 / c_H(+)^2) = c_Y und durch Auflösen nach c_H2Y: c_H2Y = c_Y / (1 + KS1 / c_H(+) + KS1 * KS2 / c_H(+)^2) Auf analoge Weise erhält man für c_HY(-) und c_Y(2-): c_HY(-) = c_Y / (c_H(+) / KS1 + 1 + KS2 / c_H(+)) c_Y(2-) = c_Y / (c_H(+)^2 / (KS1 * KS2) + c_H(+) / KS2 + 1) c) Dreibasige Säuren Durch Kombination der 3 Gleichgewichtsbeziehungen für KS1, KS2 und KS3 erhält man 3 zusätzliche Beziehungen für KS1 * KS2, KS2 * KS3 und KS1 * KS2 * KS3. Aus diesen insgesamt 6 Gleichungen gewinnt man durch Auflösen nach jeweils einer der Konzentrationen für die protonierten Säurereste 4 mal 3 Beziehungen zwischen jeweils 2 Säurerestkonzentrationen. Mit Hilfe dieser 12 Beziehungsgleichungen können wiederum die Berechnungsgleichungen für die Konzentrationen der 4 unterschiedlichen Säurereste in Abhängigkeit von c_H(+) erstellt werden. Die Ausführung dieser Fleißarbeit, sowie die Erstellung der 5 Gleichungen für eine vierbasige Säure nach demselben Prinzip, sei dem Leser selbst überlassen. |
|
Gästebuch Impressum Datenschutz Disclaimer Zitationsregeln Layout |